Beyond Linear Modeling using R (part-2)

In a previous post we fitted a non linear model to some randomly generated data. Here we will a different type of non-linear function and evaluate the results.

Modeling

In this approach we will model the same data generated by the previous post but the relationship between x and y will be modeled with an exponential function:

With the following script we will directly fit an exponential model using again the nls() function.

# exponential model fit
> expmodel <- nls(y ~ I(exp(1)^(b + a * x)), data = ds, start = list(b = 0,a = 1), trace = F)
# summary of coefficients
> summary(expmodel)$coefficients

   Estimate Std. Error   t value     Pr(>|t|)
b -4.114140  0.1802758 -22.82137 1.239745e-19
a  4.214029  0.1998630  21.08459 1.010778e-18

The model estimated that b = -4.114140 ± 0.1802758 and a = 4.214029 ± 0.1998630. Additionally, both of these variables are highly significant (p << 0.05).

Plotting

Plotting the fitted model and the cubic approximation we have the following graph:

>plot(y ~ x, main = "Fitted exponential function")
>s <- seq(0, 1, length = 100)
>lines(s, s^3, lty = 2, col = "red")
>lines(s, predict(expmodel, list(x = s)), lty = 1, col = "blue")
>legend("topleft", legend=c("fitted exponential", "cubic"),
       col=c("blue", "red"), lty=1:2, cex=0.8, box.lty=1, box.lwd=1)

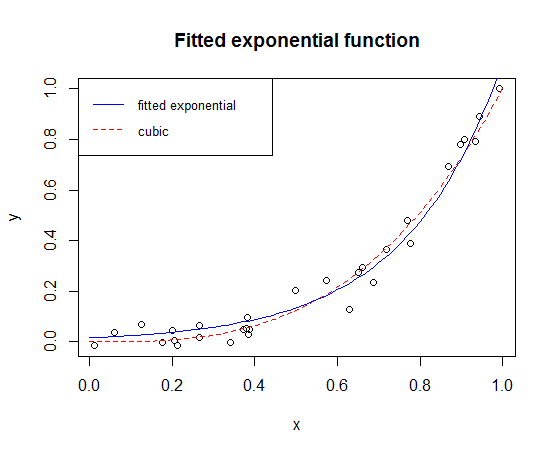
We can see that the fitted model is close to the cubic model that we used initially.

Goodness of fit

To examine the goodness of fit of the model, we will calculate R squared, seen in a previous post for linear regression:

# sum of squared error
> SSE <- sum(residuals(expmodel)^2)
# total sum of squares 
> SST <- sum((y - mean(y))^2)
# Rsquared
> Rsquared_exp <- 1-(SSE/SST)

R squared is calculated at 0.9764 which is a very good result highlighting the overall good performance of the model. Also, it is slightly smaller than the respective measure of the power model used in the previous post.