17 Jan Linear Regression Summary Statistics
Continuing from the previous post where we used an indicative dataset to perform a linear regression to it, we will elaborate on some useful statistical figures returned by the function summary() in R when applied to an lm() object holding a linear regression model.
In our case, the results of the function summary() when applied to a linear_mod are the following;
>summary(linear_mod) Call: lm(formula = dist ~ speed, data = cars) Residuals: Min 1Q Median 3Q Max -29.069 -9.525 -2.272 9.215 43.201 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -17.5791 6.7584 -2.601 0.0123 * speed 3.9324 0.4155 9.464 1.49e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 15.38 on 48 degrees of freedom Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438 F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
Evidently, the result of the summary function highlights 4 main components;
- Call which shows the fuction used in the built regression model
- Residuals which describes the distribution of the residuals based on median, min, max values as well as Q1 and Q3 quartiles.
- Coefficients shows the estimated w coefficients of the linear regression model along with their statistical significance. The more significant they are, the more strong evidence we have that the respective predictors are important for the response variable.
- R-squared, F-statistic and Residual Standard Error(RSE) are goodness of fit metrics.
Regarding the Coefficients component, for a given predictor its t-statistic (and its correspondent p-value) measure the statistical significance of the predictor, or in other words, whether or not the w coefficient is significantly different from zero. Generally, a small p-value, smaller than a significance level of 0.05, is a good evidence that the predictor we are looking on is significant for the estimation of the response variable.
R-squared is a metric sowing the proportion of variation in the data that can be explained by the model. The values of this metric is between 0-1 and the larger the value the better the constructed model. The formula that calculates R-squared is the following;
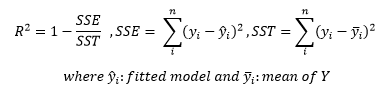
The Residual Standard Error (RSE) shows the residual variation i.e. the average variation of the observations points around the fitted regression model. The formula that calculates RSE is;
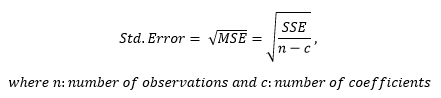
The F-statistic highlights the overall significance of the model and it assess whether at least one predictor variable has a non-zero value. The formula for thsi metric is the folowing;
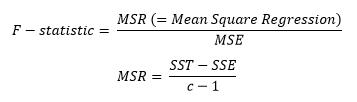



Sorry, the comment form is closed at this time.