Exploratory Data Analysis – Central tendency

Exploratory data analysis (EDA) is an important first step when getting to know better the data we have to analyze. Here we summarize some basic metrics that can be used in order to get a better view of the data.

Central tendency

Is a central or typical value of a probability disrtibution. Common measures of central tendency are mean, median and mode. Assuming that we have n data values labeled x1 through xn, the formula for calculating the sample (arithmetic) mean is:

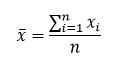
The arithmetic mean is simply the sum of all of the data values divided by the number of values. When a the distribution is symmetric, then the mean value is the middle value. When the distribution is not symmetric then the mean value is the “balance point” where it seperates the distribution in two equal weighted parts.

The median is another measure of central tendency and is calculated by the middle value after all of the values are put in an ordered list. If there are an even number of values, then the average of the two middle values is the median. This metric is particularly robust when there are extreme values in the data.

Another measure of central tendency is the mode which is the most likely or frequently occurring value. More commonly we simply use the term “mode” when describing whether a distribution has a single peak (unimodal) or two or more peaks (bimodal or multi-modal). In symmetric, unimodal distributions, the mode equals both the mean and the median. In unimodal, skewed distributions the mode is on the other side of the median from the mean. In multi-modal distributions there is either no unique highest mode, or the highest mode may well be unrepresentative of the central tendency. For discrete distributions, since the probability mass function can take its largest value in multiple points, it is possible that the mode may not be unique or representative (e.g. the uniform distribution).