Two Sample t-Test

In this posts we will discuss about another variation of t-test family of statistical tests; the two-sample t-test.

definition

Two sample t-test is used to compare the means of two independent samples (mA and mB). For example we draw randomly from a population 200 individuals, 100 men and 100 women and measure their height. The goal is to determine whether the difference in height is significant among these two groups.

The common research questions the one sample t-test attempts to answer are the followings:

• Is the mean mA equal to mB ?
• Is the mean mA larger than mB?
• Is the mean mA less than mB?

Therefore, the two-sample t-test constructs the following hypotheses in order to answer the afforementioned research questions. The null hypothesis is as follows;

• H0: mA=mB (two-tailed)
• H0: mA≥mB (one-tailed)
• H0: mA≤mB (one-tailed)

The respective alternative hypothesis is constructed as the following;

• H0: mA≠mB
• Η0: mA<mB
• Η0: mA>mB

formula

The formula for the t-statistic can be calculated as follows:

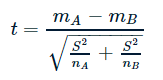
where mA, mB: the mean of sample A and sample B respectvely,

S: the pooled standart deviation with nA+nB-2 degrees of freedom (calculation shown below) and

nA, nB: the size of sample A and B.

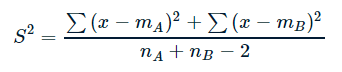
assumptions

As a parametric procedure, the two-sample t-test makes several assumptions;

• The dependent variable should be approximately normally distributed for both samples. One can verify this with many ways: inspecting the Q-Q plot or implementing the Shapiro-Wilk test are some of them.
• The two samples are independent. There is no relationship between the individuals in one sample as compared to the other.
• The variances of the two populations are equal. This can be tested using the variance ratio F-test.

procedure

After calculating the mean of the samples and the standard deviations as well as the test statistic, the p-value (i.e. the probability of observing the test statistic or a more extreme value, under the null hypothesis) can be calculated as follows;

• p = 2 ⋅ Pr(T > |t|)  (two-tailed)
• p = Pr(T > t)    (upper-tailed)
• p = Pr(T < t)    (lower-tailed)

interpretation

As a rule of thumb, a large p-value indicates a strong probabbility that a similar t-statistic can be observed. Thus the null hypothesis can be supported by the statistical test. On the other hand, a small p-value indicates a decreased support for the null hypothesis. However, the possibility that a very rare value is obtained and that the null hypothesis is true can never be ruled out completely. The threshold for determining statistical significance is usually a value of 0.05 or less.